Support Vector Regression
이 포스트에서는 Support Vector Regression(SVR) 의 개념을 이해하고자 합니다. 간단한 형태의 데이터를 이용하여 SVR 의 요소들이 어떠한 의미를 가지고 있는지 확인해 보도록 하겠습니다.
아래 내용은 고려대학교 강필성 교수님의 Business-Analytics 강의와 Support Vector Regression 논문(Basak, D., Pal, S., & Patranabis, D. C. , 2007), 평가를 위하여 Scikit-learn 의 SVR 코드와 고려대학교 DMQA 연구실 박사과정 이민정님의 SVR 코드를 참고하여 작성되었습니다. 잘못된 부분이 있으면 연락 바랍니다. - changhyun1.lee@gamil.com
Sample Data
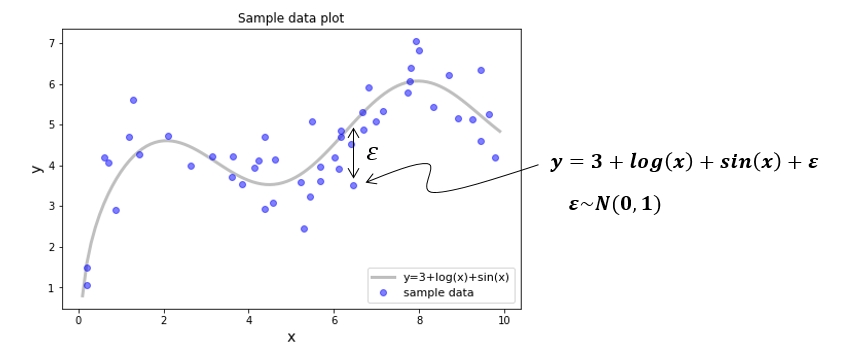
𝒚=𝟑+𝒍𝒐𝒈(𝒙)+𝒔𝒊𝒏(𝒙) 의 식에 정규분포를 따르는 노이즈를 주어 50개의 샘플 데이터를 생성하였습니다. 이 샘플 데이터를 이용하여 SVR 이 어떤 원리로 작동되는지 알아보도록 하겠습니다.
Linear Regression
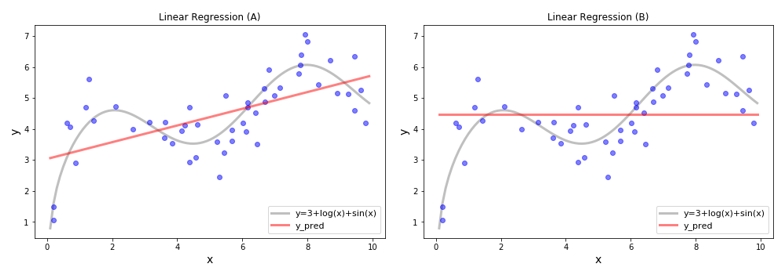
SVR 을 진행하기 전에 Linear Regression 부터 확인해 보도록 하겠습니다. Sample 데이터를 이용하여 𝒚=𝜷0+𝜷1𝒙 의 식을 얻을 수 있으며 아래와 같은 회귀선을 구할 수 있습니다. 그러면 (A) 와 (B) 의 차이는 무엇일까요? (A) 는 최소제곱법으로 찾은 오차를 최소화 하는 𝜷0와 𝜷1을 가지는 회귀식이고, (B) 는 𝜷0=평균, 𝜷1=0 인 회귀선 입니다. 어떤 회귀식이 더 좋은 회귀식 일까요? 일반적으로는 (A) 가 오차가 더 작으니 좋은 회귀식으로 말할 수 있습니다.
Prediction New Data
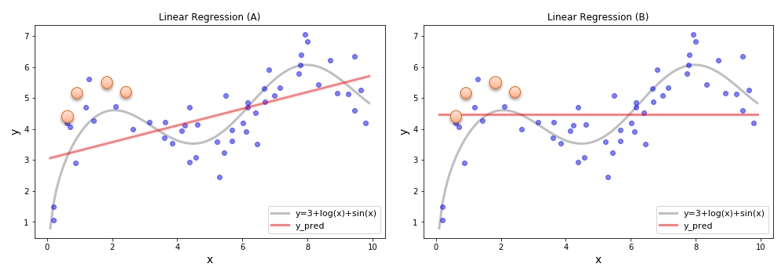
조금 과장을 하여 아래와 같은 새로운 데이터들이 주어질 경우 누가 더 예측을 잘할까요? (B) 가 아마도 더 낮은 오차로 예측을 할 것 입니다. 왜 이런 일이 생겼을까요? (A) 가 주어진 데이터에 과적합(overfit) 되어 있어서 그렇습니다. 전체의 데이터 분포가 아닌 현재 가지고 있는 데이터를 이용하여 학습하였기 때문에 현재 가지고 있는 데이터만 잘 설명하고 있습니다. 따라서 새로운 데이터를 어느 정도로 예측할 수 있을지는 장담하기 어렵습니다. 이러한 일을 방지하기 위해서는 어떻게 해야 할까요? (B) 처럼 회귀식의 기울기를 작게 하는 것입니다. 회귀식의 기울기를 작게 한다는 것은 입력 변수 𝒙 에 따른 민감도를 줄이는 것입니다. 다시 말해서 예측값의 variance 를 줄이는 것입니다.
Ridge Regression
입력 변수에 대한 민감도를 줄여 과적합을 막아 모델의 Variance 를 낮출수 있는 방법으로 Ridge Regression 이 있습니다. 입력 변수에 대한 민감도를 줄이기 위해 Linear Regression 의 Loss function 에 계수의 크기를 제약식으로 추가한 방법입니다. 이를 통하여 오차도 적당히 줄이면서 민감도도 낮은 과적합이 개선된 예측 모델을 얻을 수 있습니다. Ridge Regression 의 loss function 은 다음과 같이 나타 낼 수 있습니다.
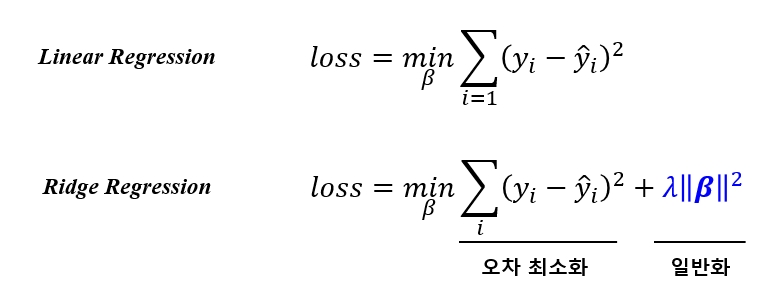
SVR - Fomulation
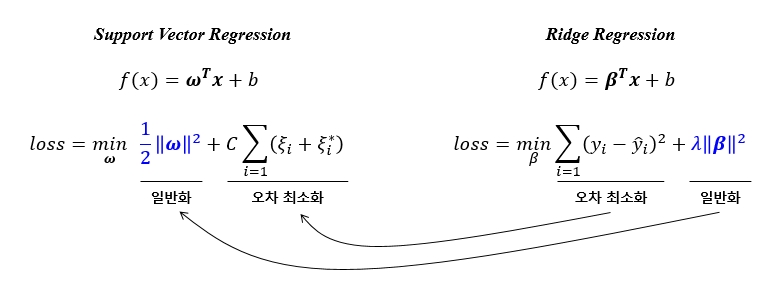
Support Vector Regression 은 위에서 살펴본 Ridge Regression 과 상당히 유사합니다. SVR 과 Ridge 의 함수식과 loss function 을 비교해 보면 아래와 같습니다. SVR 의 loss function의 각항을 Ridge 의 loss function 과 비교하여 보면 SVR 의 loss function 이 가지는 의미를 쉽게 이해할 수 있습니다. 결국 C 값에 따라 오차도 최소화하면서 계수의 크기도 작은 일반화 된 회귀식을 찾을 수 있습니다.
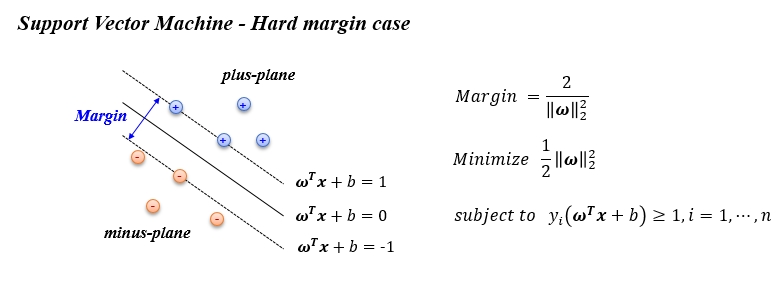
SVM - Hard Margin
그럼 SVR 의 loss function 이 어떤 과정을 거쳐 생성이 되었는지 알아보겠습니다. 이를 위하여 SVM 의 hard margin 과 soft margin 을 이해할 필요가 있습니다. SVM 에서 좋은 분류기준선을 얻기 위하여 margin 을 크게 하는 것이 중요한데, 계산의 편의를 위하여 margin 의 역수를 최소화 하는 최적화 문제를 풀게 됩니다. 이때에 제약조건은 ‘+’ 인 데이터는 plus-plane 에 ‘–’ 인 데이터는 minus-plane 에 들어가야 합니다. 다시말해서 ‘+’ 데이터가 minus-plane 에 들어가서는 안됩니다.
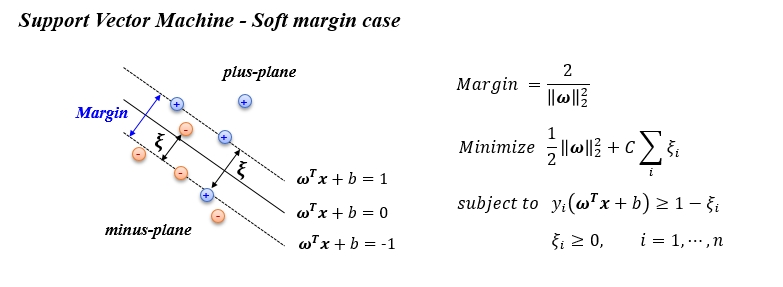
SVM - Soft Margin
이번에는 SVM 의 Soft margin case 를 살펴 보도록 하겠습니다. Hard margin 과 달리 ‘+’ 데이터가 plus-plane 밖에 있는 것을 허용해 줍니다. 무한정 허용해 주는 것은 아니고 밖에는 있으되 최대한 가깝게 있으라는 제약을 걸어줍니다. 이로써 몇 개의 데이터는 분류 오류가 생기지만 전체적으로 margin 이 큰 분류선을 얻을 수 있게 됩니다.
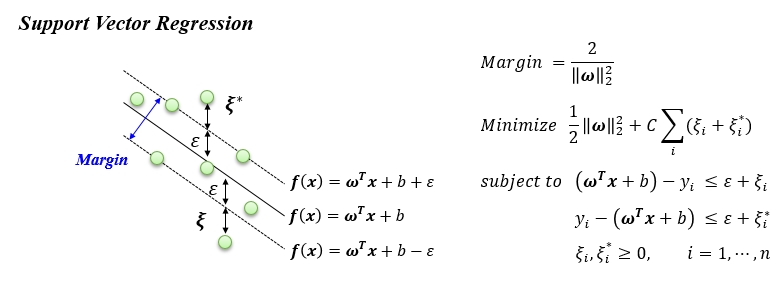
SVR vs SVM
SVR 은 SVM 의 Soft margin case 와 유사합니다. SVR은 모든 데이터를 epsilon tube 안에 두고 싶어 합니다. 하지만 epsilon tube 의 크기는 정해져 있기 때문에(hyper-parameter) 모든 데이터가 tube 안에 들어갈 수는 없습니다. 이 때 tube 밖에 있는 데이터는 최대한 tube 가까이에 있어야 한다는 제약을 걸어 줍니다. 이로써 우리가 원하는 최적의 회귀식을 구할 수 있습니다.
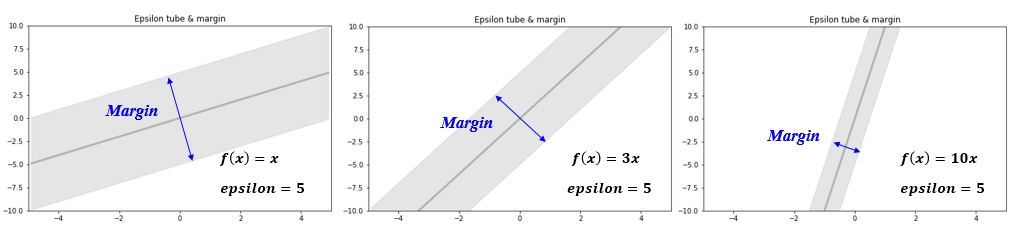
Margin - Epsilon tube
SVR 에서 epsilon tube 의 크기와 margin 의 관계에 대하여 이해를 돕기 위하여 아래 그림을 보도록 하겠습니다. 아래 그림들은 모두 같은 epsilon 값을 가지지만 tube 의 크기인 margin 은 차이가 있습니다. 회귀식의 기울기가 커질수록 margin 은 작아지게 됩니다. 이렇게 되면 많은 데이터들이 밖으로 나오게 되어 error의 합이 커지게 됩니다. 따라서 기울기는 작아져야 합니다. 무작정 작아지면 되는 것은 아니고 작아지면서 error 의 합도 작아져야 한다는 것입니다. 결국 margin 을 최대화 한다는 것은 기울기를 작게 하겠다라는 의미 입니다. 기울기를 작게 하겠다는 의미는 결국 입력 변수에 대한 민감도를 줄이는 것이고 모델의 variance 를 낮추는 개념입니다. 이러한 개념은 Ridge 와 동일하다고 할 수 있습니다.
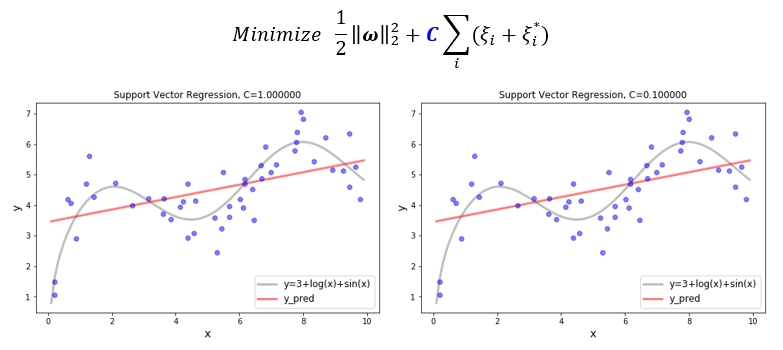
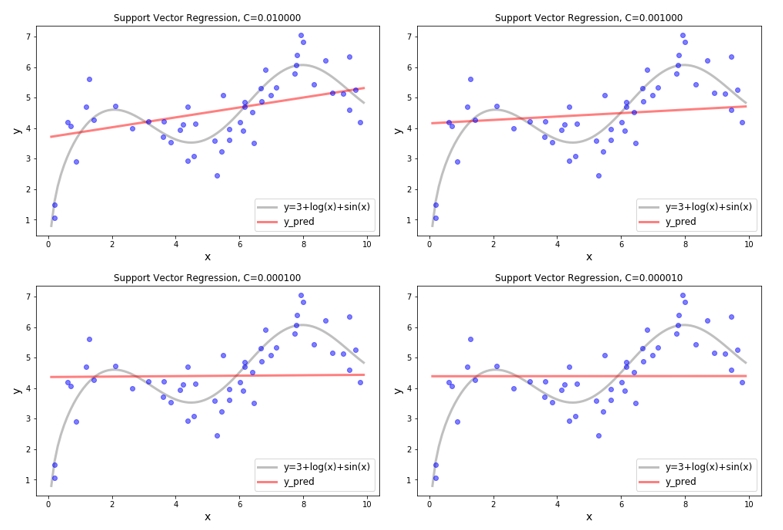
SVR - C
SVR 의 목적함수를 다시 보도록 하겠습니다. C 값에 따라서 오차의 합을 중요하게 생각할지 무시할지 결정할 수 있습니다. 위에서 보았던 샘플 데이터를 이용하여 C 값이 변함에 따라 회귀식이 어떻게 변하는지 확인해 보겠습니다. 아래 그림을 보면 C 가 1에서 0.00001 까지 줄어드는 과정에서 회귀식의 기울기가 작아지고 있습니다. 오차의 합을 중요하게 생각하지 않으면 (C=0.00001) margin 이 커지면 되는 것이니, 기울기는 0으로 수렴하게 됩니다.
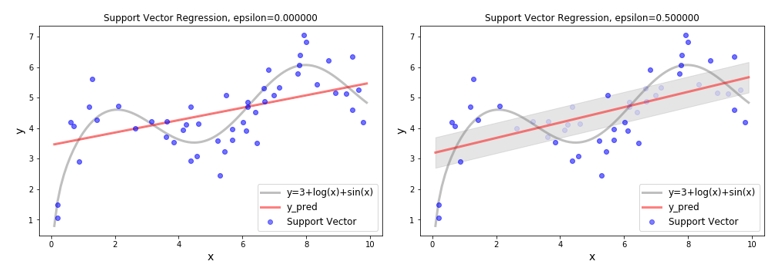
SVR - Epsilon
이번에는 epsilon 의 크기에 따라 회귀식이 어떻게 변화 되는지 확인해 보도록 하겠습니다. Epsilon 값이 커진다는 것은 튜브 밖에 있는 데이터의 수가 적어진다는 것을 의미합니다. 그럼 고려되어야 할 데이터의 수도 작아집니다. 전체를 다 이용하지 않고 몇 개의 데이터로 회귀식을 학습하더라도, 비슷한 기울기의 회귀식을 얻을 수 있다면 몇 개의 데이터만 사용하는 것이 더욱 효율적일 것입니다. 여기서 SVR 의 계산 효율성을 확인 할 수 있습니다. 그렇다고 해서 epsilon 값이 크다고 무조건 좋은건 아니니 적절한 epsilon 값을 선택하는 것이 중요합니다.
Convex optimization Problem
이제 SVR 에 대한 이해가 어느정도 되었으니 수식으로 최적해를 구하는 과정을 살펴보도록 하겠습니다. Original problem 을 풀기 위해서 lagrangian multiplier 를 이용하여 lagrangian primal 식을 만들수 있습니다. KKT condition 의 stationarity 조건에 따라 각 변수로 편미분한 값이 0인 지점이 primal 의 최소값이며 동시에 dual 의 최대값입니다. 굳이 dual 로 문제를 변형하는 이유는 누가 봐도 dual 식이 푸는데 더 쉬워보이니 그런것이라고 생각하면 편할것 같습니다. 실제로 primal 에서는 찾아야할 변수가 𝑏, 𝜔, 𝜉, 𝛼, 𝜂 인 반면에 dual 에서는 𝑏, 𝛼 만 찾으면 됩니다. 또한 𝛼 의 2차항으로 나타나기 때문에 convex, continuos 이므로 전역최적해가 존재하므로 dual 문제로 변형하여 해결합니다. 수식은 아래를 참고하시길 바랍니다.

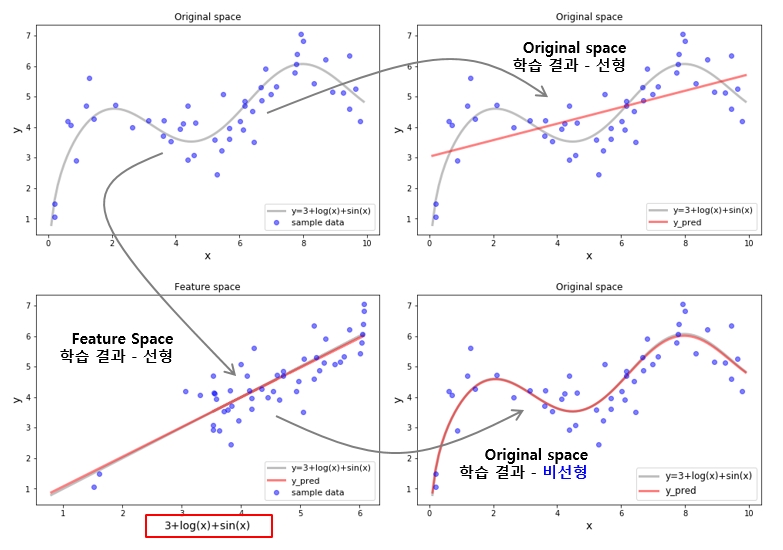
Feature space, mapping
지금까지 구한 회귀식은 선형식으로 원 데이터가 비선형 구조라고 하면 이를 설명하는데 한계가 있습니다. 이를 극복하기 위해서 데이터를 고차원의 feature space로 mapping하여 학습을 진행 합니다. Original space 에서는 선형으로 해석이 안되던 부분이 고차원의 feature space 에서는 선형으로 분리될 수 있기 때문입니다. Original space 의 데이터를 고차원의 feature space 로 보내기 위해서는 mapping 함수가 필요합니다. 예를 들어 위에서 사용한 샘플 데이터의 𝒙 를 𝟑+𝒍𝒐𝒈(𝒙)+𝒔𝒊𝒏(𝒙)로 mapping 하게 되면 비선형 관계에 있던 데이터들이 선형 관계로 변하게 되어 선형으로도 충분히 정확한 모형 학습이 가능합니다.
Kernel trick
하지만 이러한 맵핑함수를 모르더라도 kernel 함수를 이용하면 효율적으로 데이터를 고차원의 feature space 로 변환할 수 있습니다. 위의 수식으로 확인한 Lagrangian Dual 의 함수식에서 x 의 내적부분을 Kernel 함수로 바꾸는 것만으로도 고차원 feature space 에서 학습되는 효과를 가질 수 있습니다. 아래는 kernel 함수의 예를 나타낸 것입니다. Kernel 선택은 딱히 기준이 없기 때문에 사용하는 데이터의 특성에 맞는 kernel 을 선택하는 것이 중요합니다. 일반적으로 RBF Kernel 이 많이 사용 됩니다.

SVR - C with RBF Kernel
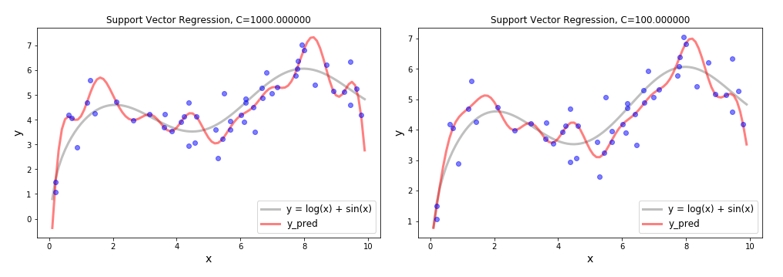
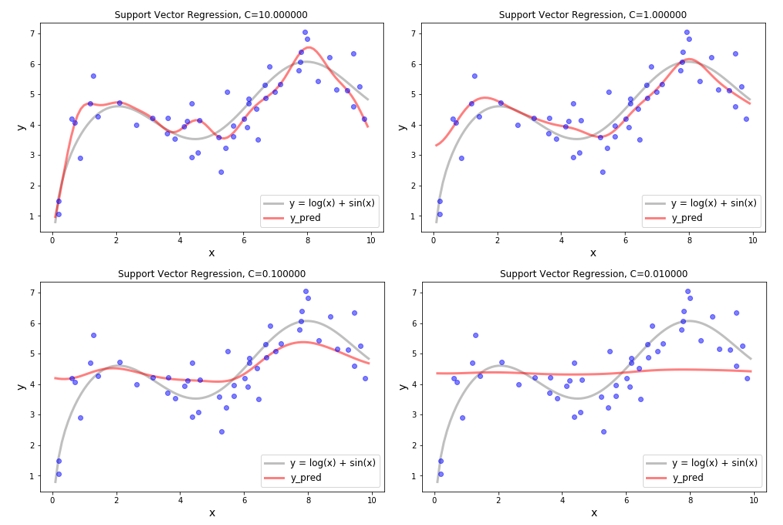
아래는 RBF Kernel 을 사용하여 SVR 모델을 학습한 결과입니다. SVR 은 기본적으로 선형 모델이지만 고차원의 feature space 에서 선형으로 학습 하였기 때문에 original space 에서는 곡선으로 학습된 것 처럼 보일 수 있습니다. 이점이 kernel 을 사용하는 이유 입니다. 선형 학습 결과와 동일하게 C 값의 크기에 따라서 일반화가 이루어지는 것을 확인할 수 있습니다. C 값이 클 경우 과대적합(overfit) 양상이 확인되며, C 값이 작을 경우 과소적합(underfit) 양상이 확인 되므로 적절한 C 값을 사용하는 것이 중요합니다.
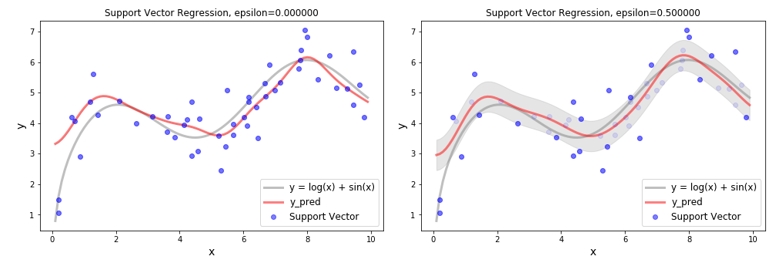
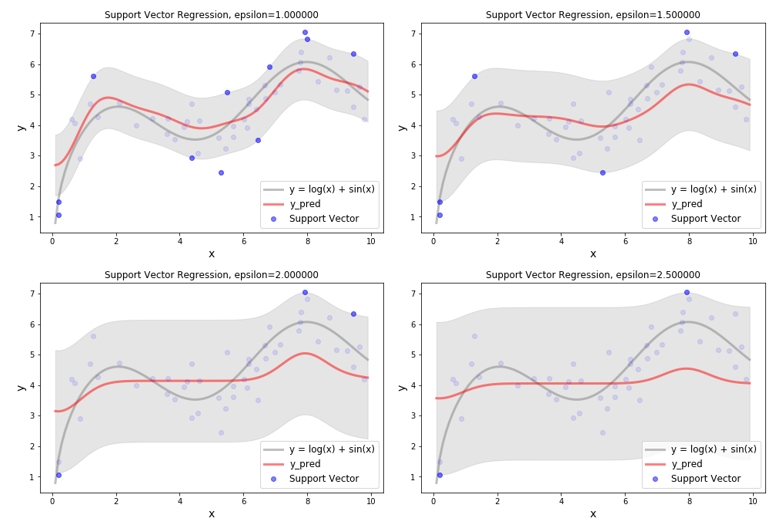
SVR - Epsilon with RBF Kernel
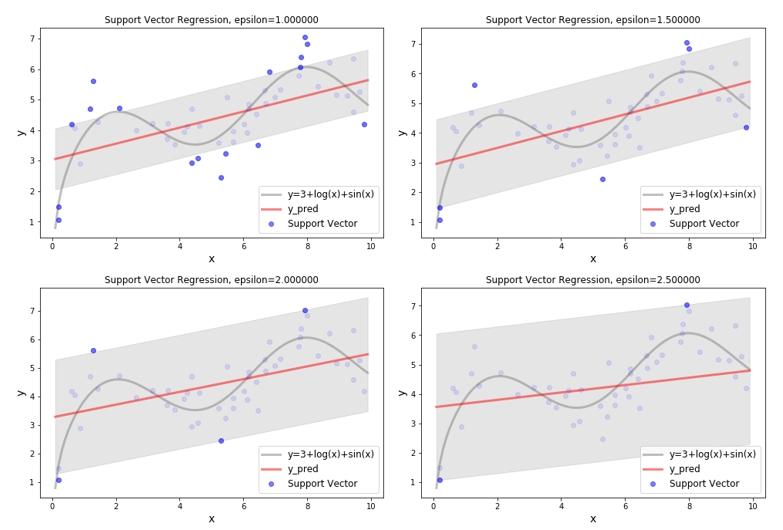
마찬가지로 epsilon 에 대해서도 확인해 보았습니다 이때의 C 값은 1 입니다. Kernel 을 사용하지 않았을 때에는 epsilon 이 커지더라도 유사한 형태의 회귀 결과를 보였었는데, kernel 을 사용 후 epsilon 이 커짐에 따라서 underfit 양상이 보입니다. 물론 이러한 양상은 데이터에 따라서 달라질 수 있으니 본 내용에서는 전체적인 흐름만 참고 하면 될 것 같습니다.
RBF Kernel - Gamma
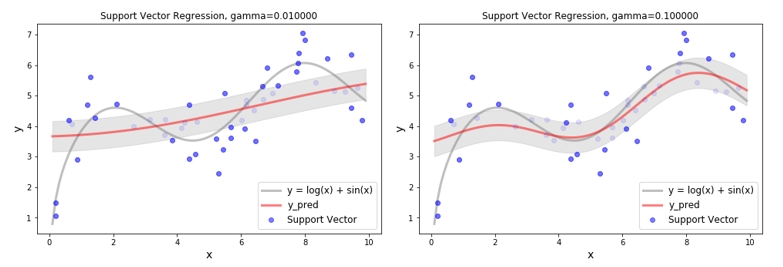
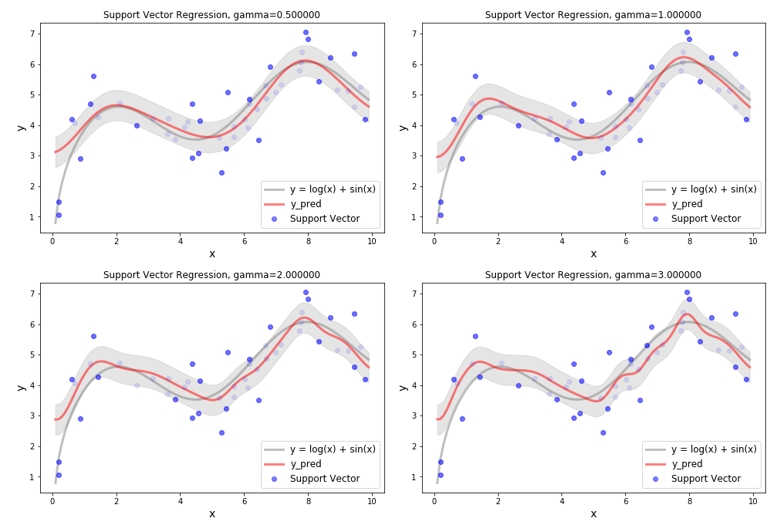
다음은 C=1, epsilon=0.5 일때, RBF kernel 에 있는 𝛾 값을 변화 하면서 회귀식의 변화를 확인한 것입니다. 𝛾 값이 크다는 것은 두 벡터 사이의 거리를 더 크게 보겠다는 의미이고, 𝛾 값이 작다는 것은 두 벡터 사이의 거리를 작게 보겠다는 의미 입니다. 즉 RBF kernel fuction 에 의해 생성되는 고차원의 feature space 가 𝛾 값이 크면 넓게넓게 생성되고 𝛾 값이 작으면 조밀조밀 하게 생성이 되는 것이죠. 넓게넓게 생성이 되면 아무래도 데이터를 좀더 자세하게 학습을 할 것이고 조밀조밀하게 생성이 되면 단순하게 학습을 할 것 같습니다. 이런 상황을 아래 그림에서 확인 할 수 있습니다. 따라서 일반화 성능을 향상시키기 위해서 적당한 𝛾 값을 사용하는 것 또한 중요합니다.
Various Loss function for SVR
각 데이터가 가지는 error를 아래와 같은 loss function 으로 사용할 수 있습니다. 지금까지 평가한 내용은 가장 기본적인 𝜺−𝒊𝒏𝒔𝒆𝒏𝒔𝒊𝒕𝒊𝒗𝒆 loss function 을 사용한 결과입니다. 절대적으로 좋은 모델이란 없듯이 loss function도 마찬가지인것 같습니다. 필요에 따라 회귀식에서 가까이 있는 데이터와 멀리 있는 데이터의 loss 에 다른 가중치를 주고 싶을때 아래 그래프를 참고하여 원하는 형태의 loss function 을 선택하여 사용하면 좀 더 사용자의 의도가 더 잘 반영된 회귀식을 찾아 낼 수 있다 정도로 생각하면 될 것 같습니다.
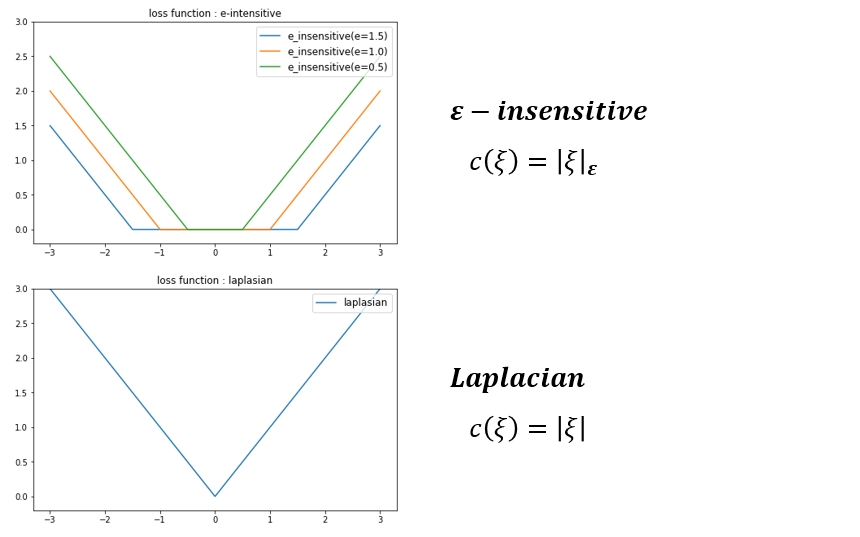
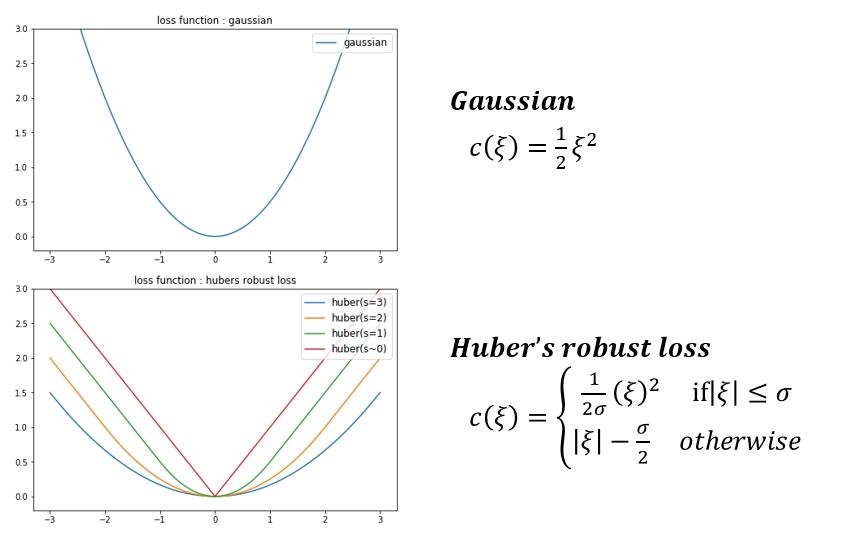
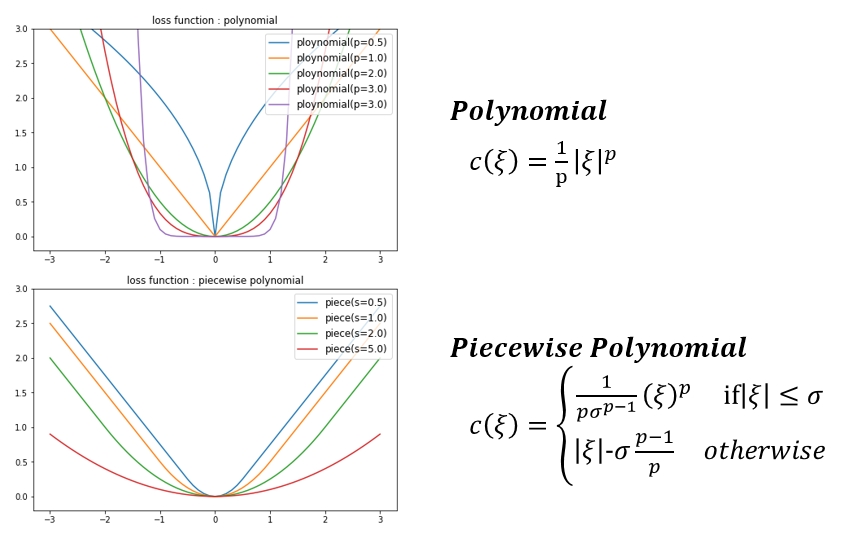
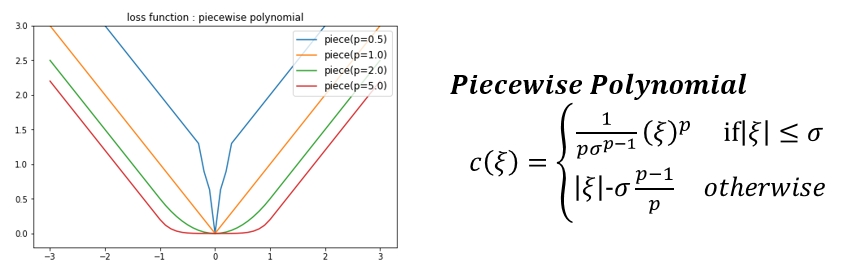
SVR - Various Loss function
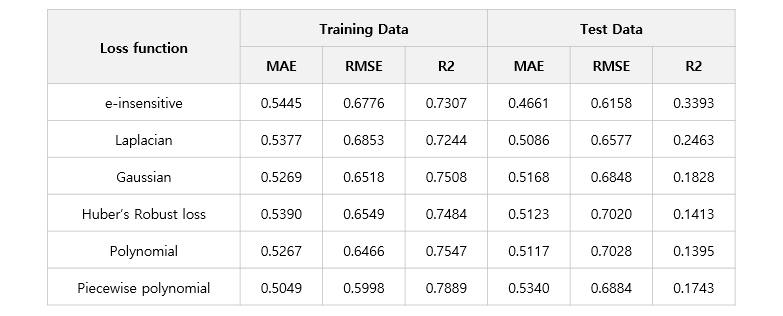
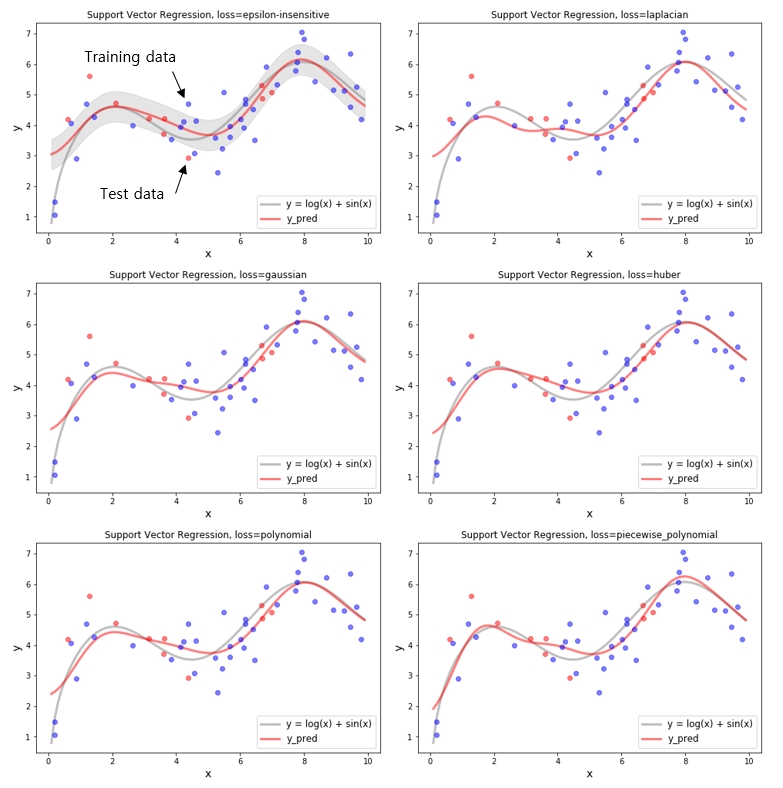
위에서 본 여러가지 loss function 을 이용하여 SVR을 학습 시킨 결과는 아래와 같습니다. 뭔가 드라마틱한 차이를 기대했지만 샘플 데이터로는 큰 차이를 보이지는 않습니다. 하지만 각 loss 에 따라서 살짝씩 회귀식이 변하는 것을 보면 각 데이터의 loss 에 대해 반영은 되고 있는것 같습니다. 실제 데이터에서는 더 잘맞는 loss 가 있을 수 있으니 알아 두면 좋을 것 같습니다.
Conclusion
이 포스트에서 SVR 이 어떻게 학습이 되어 어떤 결과를 내어 주는지에 대하여 살펴 보았습니다. SVR 은 epsilon tube 와 C 값을 이용하기 때문에 모델식을 일반화 하는데 유리하며, support vector 라는 필요한 몇개의 데이터만을 학습에 이용하기 때문에 계산 효율성에도 유리합니다. 또한 convex optimization problem 이므로 항상 최적해를 구할 수 있다는 장점도 있습니다. SVR 은 선형의 최적해를 구하지만 kenel 을 이용하여 비선형의 최적해도 충분히 찾을 수 있다는 점도 확인하였습니다.
본 포스트에서 사용한 code 는 github page 에 있으니 참고바랍니다. (https://github.com/Changhyun-Lee/study)
감사합니다.